佐賀の印象はいかがでしょうか?

佐賀は住みやすいところだと思っています。
育ったところは神奈川県鎌倉市です。研究集会で佐賀に来たことはありましたが、まさか赴任するとは思っていませんでした。
この道の先生になろうと思ったきっかけは?

数学に取り組んでいるうちに、研究してみたいと思うようになりました。ちょっと遅いですが、本気で数学をやりたいと考えたのは大学2年の進学振り分けの時です。いろんな分野の勉強をしましたが、一番興味が持てたのが数学でした。第一希望に数学だけで出して、他の希望は出しませんでした。それまでは、数学は好きでも勉強を続けることは難しいだろうと思っていたのですが、やっぱりやってみたくて数学の道に進むことを決心しました。
数学に興味を持った大きなきっかけというのはありませんが、高校と違って大学では自分で考えることが多く面白いと思いました。例えば、高校では、「連続性」については「こういうグラフは連続です」、「極限」については「nを限りなく大きくしていくと一般項 1/n は限りなく 0 に近づいていきます」という説明がなされて終わりですが、大学になると、自分で考えながら、すごく厳密に定義していきます。「覚えること」から「自分で考えて定義する」という学びのスタイルのギャップを面白く思ったのがきっかけといえばきっかけだと思います。また、大学では先生方がとても楽しそうに授業をされたり、研究の話をしてくださったり、そういうところにも興味を引かれたと思います。
大学の教員になってよかったこと。

学生さんと触れ合うことができてとても楽しいと感じています。学生さんが質問してくれて、こちらの説明を理解してくれたときは嬉しいです。質問があるとこちらの理解も深まりますし、説明の仕方もこう言った方がわかってくれるかなと考えたりして、学生さんから刺激をもらっています。
学生たちにひとこと。

大学時代というのは自由になる時間がありますから、自分が一番興味の持てることを探す時期だと思います。いろんなことに挑戦して、自分はこれが一番やりたいと思うことを見つけて欲しいと思っています。
学生たちに読んで欲しい本をあげるとしたら。

学生のうちに読めるような長くて難しい古典などの長編小説に挑戦して欲しいです。
先生の「好きなこと」は?

私の気分転換方法は数学なんです。ちょっと自分の専門分野と違うところの基礎を勉強するのはとても気晴らしになります。散歩しながら数学の問題を考えたりします。
ご研究についてお聞かせください。

私の専門は「トポロジー」」というものです。日本語では「位相幾何学」と言います。
三角形があったとして、幾何学では二等辺三角形や直角三角形と区別をしますが、「トポロジー(位相幾何学)」では、三角形の種類で区別をしません。空間の中で、切ったり、貼ったりせずに連続的に変形して同じになるなら「同じ」だとみなすのが「トポロジー」の考え方です。ですから三角形は大きさを変えてもいいですし、どんな二等辺三角形でも直角三角形でも「同じ」となります。三角形を四角形と「同じ」だと思ってもいいですし、円周と「同じ」だと思ってもいいのです*1。
*1.トポロジーの考え方
切ったり貼ったりせず、粘土のように曲げたり伸ばしたり変形して同じになるなら同じという考え方
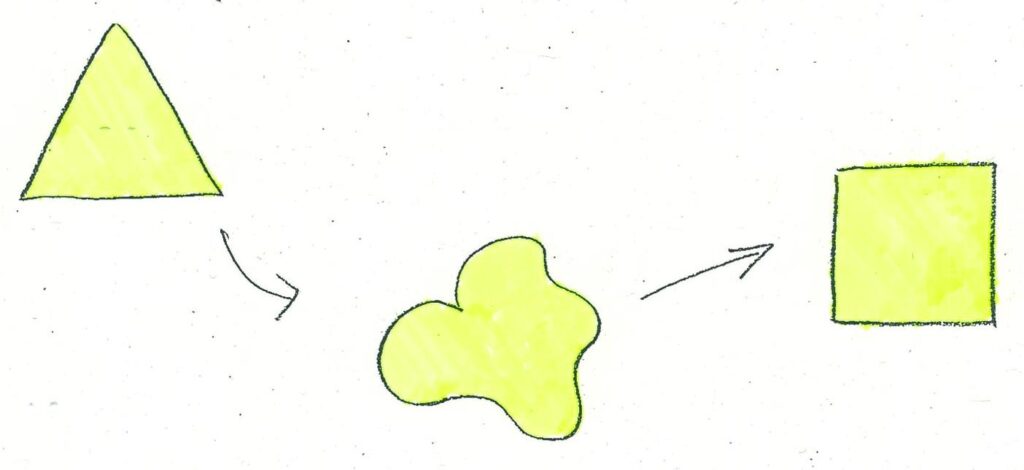

また、「トポロジー」では、「同じ」ではなく、「違う」という場合は「違う」ことを数学的に証明しないといけません。その時に使うのが「位相不変量(以下、不変量)」というものです。
「不変量」というのは、「同じ」ものに対しては同じ値を返す数学的な量のことです。数学の対象を区別できる「不変量」をなるべくたくさん構成するというのが「トポロジー」の研究姿勢です。よく言われるのが、血液型のように、同じ「不変量」を持っても「違う」場合があって、他の「不変量」で区別できるということもあります*2。
*2.血液型において、同じ不変量の血液型(ABO型)であっても違う血液型の場合があり、他の不変量で区別できる場合(Rh-型)がある。
なるべく多くの「不変量」を使っていろんなものを判別できるようになりたいというのが「トポロジー」の研究です。私は「トポロジー」の中でも特に「結び目理論」という研究をやっています。

数学における「結び目」というのは、例えば一本の靴ひもの両端をつなげた「輪っか」のことを指します。「結び目理論」では「結び目」がどこの空間に入っているかというのが大事なのですが、この時、靴ひもの「輪っか(=結び目)」自体は1次元にあります。私たちが住んでいる3次元の空間の中に、この1次元の靴ひもの「輪っか」、つまり「結び目」が置かれていると考えます。
「輪っか」になった靴ひもを切らずに空間の中で動かして同じ形に変形できるものは、「同じ結び目」と考えます。「結び目理論」の研究では、「不変量」を使って、どういう「結び目」があるのか(2つの結び目が同じか、そうでないか)というのを調べていきます。
先程の一本の靴ひもの両端をつなげた「輪っか」を「自明の結び目」と言います。靴ひもの両端をつなげて、切らないとほどけない結び目をつくると、この結び目は「自明の結び目ではない」と言います。この時、「どうして「自明」ではないのか?本当に切らないといけないのか?」というのを証明するのに「不変量」を使って数学的に証明するのが、「結び目理論」です。

「結び目理論」の研究で交点が2つのものは必ず「自明の結び目」になってしまうことがわかっています。
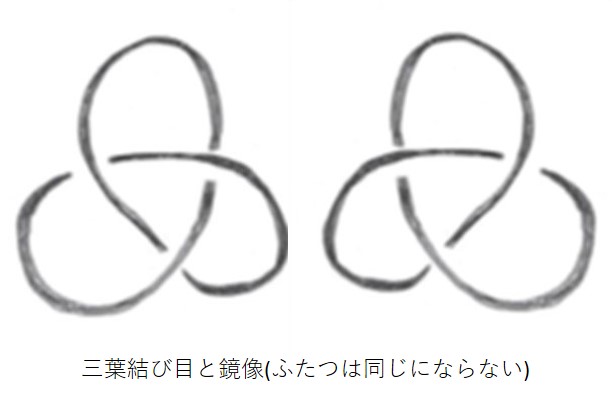
「自明ではない結び目」で一番簡単なのは交点が三つある結び目で「三葉結び目」(図A)といいます。これはひもを切らない限りほどけません。交点が3点以上ある結び目は山ほどあり、切らないとほどけない「結び目の表」があります*3。
結び目の鏡像(鏡に映した結び目)で考えたりもするのですが、「三葉結び目」の鏡像は同じではない(切ったり、貼ったりせずにひもを変形しても同じにならないし不変量も違う)ということが知られています。「8の字結び」(図B)という結び目は鏡像の場合、同じ(ひもを変形すると同じになる)になってしまうというものもあります。
結び目表の結び目は「不変量」で区別されていて、「不変量」が違うから「違う結び目」となります。きちんと証明されて増えていけばどんどん複雑になると思います。現在は、10交点ぐらいまで明らかになっていたかと思います。



これまでのお話の中の「結び目」は3次元の空間の中でのことです。3次元からもう1次元あげて4次元の空間の中にあると「結び目」が全部ほどけ、すべて「自明な結び目」になってしまいます。例えば、4次元の軸を時間とします。この4次元の空間で「三葉結び目」の交差している部分(図C:赤い部分)だけを現在から未来に移動させます。そして、交差が逆になるようにしてから、また未来から現在に赤い部分を戻すと結び目がすべてほどけてしまいます(図D)。つまり、4次元の世界では、どんなに複雑な結び目でも全部ほどくことができます。これは、3次元では不可能な操作が4次元では可能になるためです。


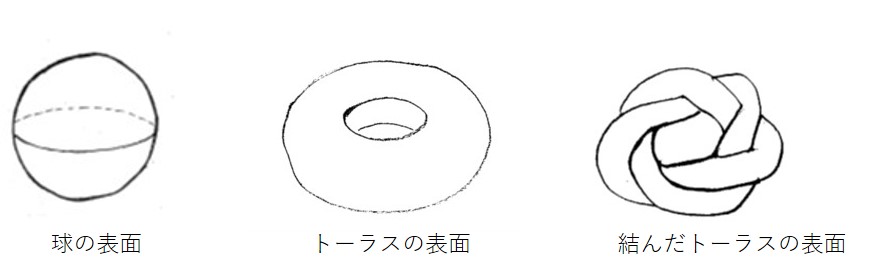
「結び目理論」の研究での私の専門は、4次元の空間の中にひもではなく「曲面」がどのように結びついているかを考える「曲面結び目」です。球面(球の表面)やトーラス(ドーナツの表面)といった図形が4次元の空間にどのように配置され、結ばれているかということを考えています。

例えば、4次元の軸を「時間軸」だとすると、「時間軸」が進むにつれて「曲面結び目」がどう変化しているかということを研究しています。4次元の軸は、4次元方向であれば、時間軸以外でもかまいません。私たちのいる3次元にある1次元の結び目というのは、点の集まりだと考えられます。
平面に点があって、時間が経つにつれて動いていって、貼り合わされるとすれば結び目ができます*4。
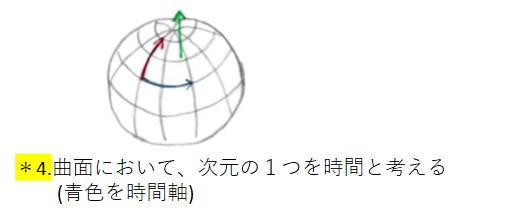

3次元(空間)×時間軸の4次元だと思えば、「自明な結び目」があったとして、時間軸に沿って動いて、貼り合わされるとトーラスというドーナツの表面の形状になります。
「曲面結び目」の研究では、「曲面結び目」を扱いやすくするための手法を考えたり、「曲面結び目」の性質について「不変量」を使って調べています。

今後の目標をお聞かせ下さい。

まず、「曲面結び目」では、「不変量」が少なく、構成例もあまりないので、よく調べたいというのが目標になっています。「面白い」というと、「どこが面白いのか?」と言われそうですが、いろいろな面白い構成例を挙げたり、「不変量」を調べてみたいと思っています。
次に「曲面結び目」で一、二連の結び目というのは「向き」がつきます。「向き」というのは、図のように矢印をつけて同じ向きにずっと進んでいけるということです(逆もあり)。「曲面結び目」は「向きがつけられるもの」と「向きがつけられないもの」とがあって「向きがつけられない方」は、まだよく調べられていないので、取り組んでみたいと思っています。
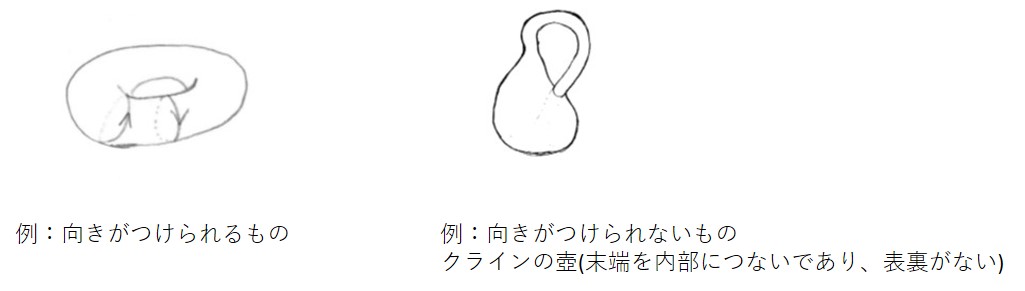

さらに、先程の「結び目表」は、3次元にある結び目を平面に表したもの(射影図)ですが、4次元の「曲面結び目」は3次元の中に射影してみることができます。曲面の集まりとして図が描けるのですが、すごく複雑になってしまうこともあります。一方で簡単な表示方法もあって、平面上に描けるような場合もありますので、研究者はそれを使って調べたりもしてます。どれくらい簡単に図を表すことができるかという点も研究対象となり得ます。
また、他の分野と連携して今の研究を発展させたいという目標もあります。
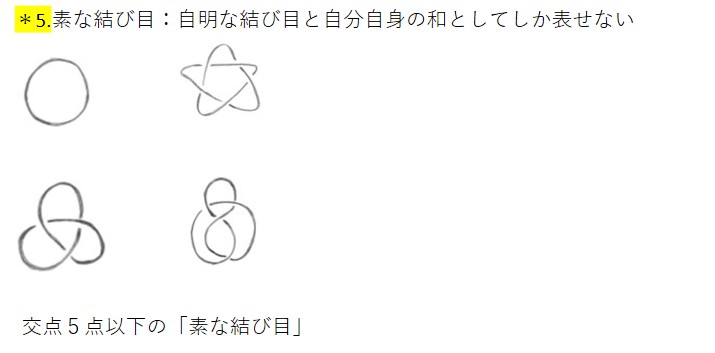
今、「整数論」と「曲面結び目」の関係性に注目しています。「整数論」という研究分野で素数を扱いますが、「曲面結び目」でも素因数分解のようなことが成り立ちます。2つの「結び目」をつないだものを「連結和」といい、分解すると、いくつかの「素な結び目」の和として一意的に表されます*5。こういった、「トポロジー」以外の分野の勉強も進めて、「曲面結び目」と関連付けていきたいと考えています。
企業・自治体・学校の中で何かやるとしたらどんなことをやりたいですか?

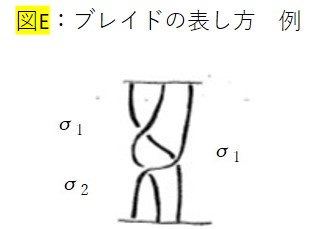
今年のオープンキャンパスで「結び⽬と組みひもの数理」というテーマで模擬授業をしました。「トポロジー」からはじめて、「ブレイド(組みひも)」について話をしました。「ブレイド」では、隣り合うひもを交差させていく様子を表すもので、それぞれのひもがどのように交差して(絡まって)いくかを考えることで「結び目」がどのように形成されるかシンプルに表すことができます。「ブレイド」では、いろいろな絡み方があり、σ1、σ2という風に記号(生成元)を使って表すことができます(図E)。

「ブレイド」は、数式や関係式で表現され、その変形を通じて「ブレイド」の性質を調べることができます。これにより、複雑な絡み合いを解析することが可能です。「ブレイド」には、代数学の基本的概念である「群構造」も重要です。群構造があることで、「同型写像(二つの構造が同じであることを示す写像)」や「準同型写像(構造を保ちながら変換する写像)」といった数学的式変形が使えますので、ブレイドや結び目の性質を詳細に調べることができます。

実生活での応用例として「ブレイド」は材料を混ぜるときの効率的な形状を考える場合などで使われていると聞いたことがあります。また、化学の化合物や原核生物のDNAは結び目を構成していたりするそうですが、現時点で具体的な応用分野はちょっと思いつきません。これからの研究活動の中で、他分野の研究者と連携したり、将来的には企業で応用(実用)に向けた取り組みができればと考えています。
取材: 2024.11.29 金曜日
参考図書
・「結び目のはなし」村上斉 1990年 遊星社
・「結び目の数学」C.C.アダムス著 金信泰造訳 1998年 培風館
・「絵ときトポロジー曲面のかたち」前原 濶・桑田孝泰著 共立出版
・平成28年度(第38回)数学入門公開講座テキスト 「結び目の数学」鈴木 咲衣
(京都大学数理解析研究所 H28.8.1~8.4開催)





